Тарг 1989 Динамика задачи Д2- Д12
- Для комментирования войдите или зарегистрируйтесь
Теоретическая механика: Методические указания и контрольные задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших учебных заведений/Л. И. Котова, Р. И. Надеева, С. М. Тарг и др.; Под редакцией профессора С. М. Тарга — 4-е изд. — М.: Высш. шк., 1989.— 111 с
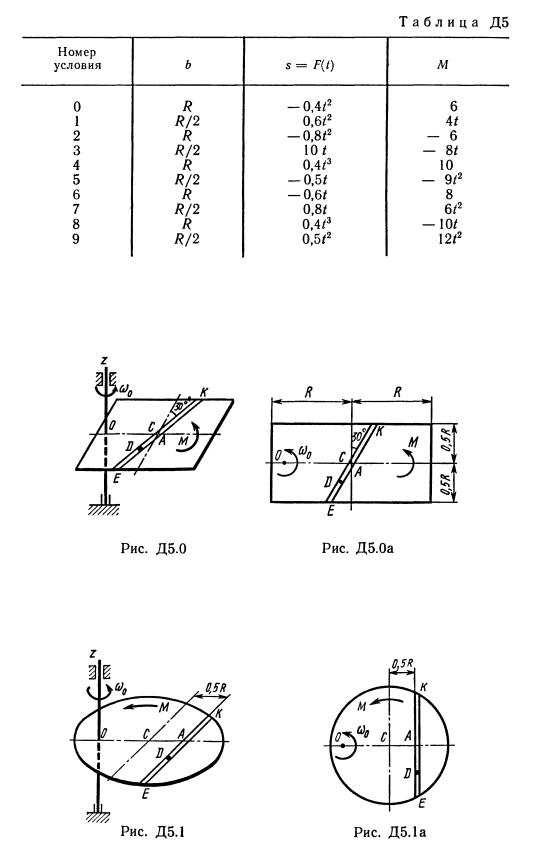
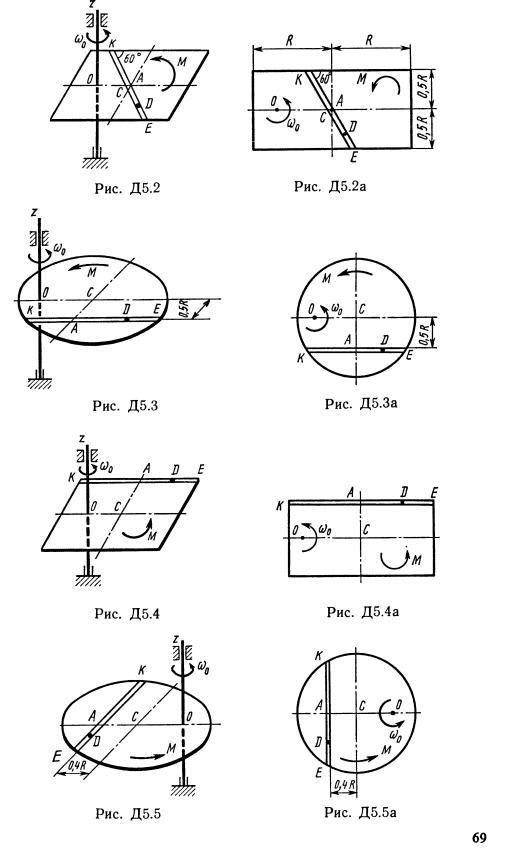
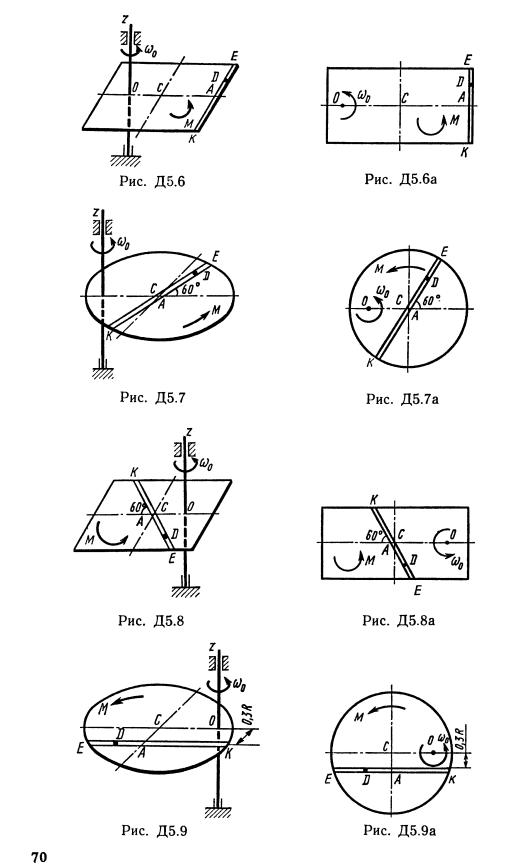
Задача Д2
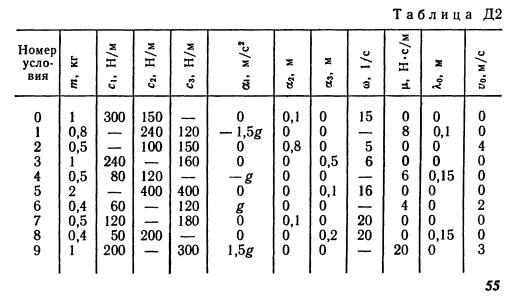
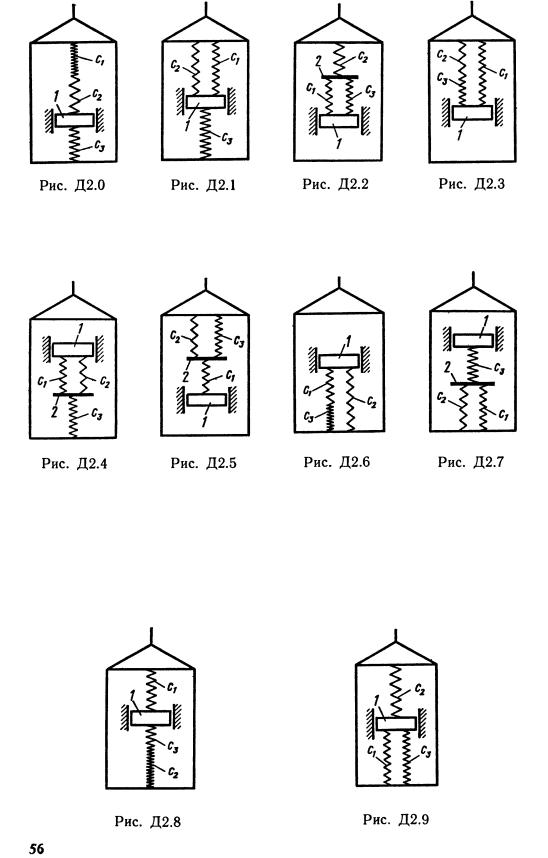
Груз 1 массой т укреплен на пружинной подвеске в лифте (рис. Д2.0 —Д2.9, табл. Д2). Лифт движется вертикально по закону z = (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = , где v — скорость груза по отношению к лифту. Найти закон движения груза по отношению к лифту, т. е. х = начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках, направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х>0, т. е. пружина растянута. При подсчетах можно принять 10 м/с2. Массой пружин и соединительной планки 2 пренебречь. В таблице обозначено: Си Сг, Сз — коэффициенты жесткости пружин, Ао — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, Vo — начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах Си С2у Сг означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие означает, что сила сопротивления R отсутствует.
Задача Д4
Механическая система состоит из прямоугольной вертикальной плиты массой 18 кг, движущейся вдоль горизонтальных направляющих, и груза D массой т2 = б кг (рис. Д4.0 — Д4.9, табл. Д4). В момент времени to = 0, когда скорость плиты ы0 = 2 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты. На рис. О—3 желоб КЕ прямолинейный и при движении груза
расстояние s = AD изменяется по закону s =/|(/), а на рис. 4—9 желоб — окружность радиуса R = 0,8 м и при движении груза угол 9=Z.y4C|D изменяется по закону <р =./2(/). В табл. Д4 эти зависимости даны отдельно для рис. О и 1, для рис. 2 и 3 и т. д., где s выражено в метрах, ф—в радианах, t — в секундах.
Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость и = /(/), т. е. скорость плиты как функцию времени.
Задача Д5
Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R, где R"= 1,2 м) массой mi = 24 кг вращается с угловой скоростью о>о = 10 с”1 вокруг вертикальной оси 2, отстоящей от центра масс С платформы на расстоянии ОС = b (рис. Д5.0 — Д5.9, табл. Д5); размеры для всех прямоугольных платформ показаны на рис. Д5.0а (вид сверху). В момент времени to = 0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой т2 = 8 кг по закону s = AD = F(t), где s выражено в метрах, t — в секундах. Одновременно на платформы начинает действовать пара сил с моментом М (задан в ньютонометрах; при М<0 его направление противоположно показанному на рисунках). Определить, пренебрегая массой вала, зависимость а> = /(/), т. е. угловую скорость платформы, как функцию времени. На всех рисунках груз D показан в положении, при котором s>0 (когда s<0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии ОС = b от центра С.
Задача Д7
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса г = 0,6/? (рис. Д7.0 — Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F\ и F2, направления которых определяются углом 0; кроме сил на барабан действует пара с моментом М; когда в таблице Ai<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона а так, как показано на рисунках. Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = /(/)* и наименьшее значение коэффициента трения / о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.
Задача Д8
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью (о= 10 с-1, закреплен подпятником в точке Л и цилиндрическим подшипником в точке, указанной в табл. Д8
в столбце 2 (АВ — BD = DE = ЕК — а). К валу жестко прикреплены тонкий однородный ломаный стержень массой т = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках,
где Ь = 0,1 м, а их массы т\ и т2 пропорциональны длинам), и невесомый стержень длиной / = 4Ь с точечной массой т3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней
указаны в таблице в столбцах 3 и 4, а углы а, р, 7, <р даны в столбцах 5—8. Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.
Задача Д9
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами а, р, у» ф» 0 (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: Л = 0,4 м, U = 0,6 м
(размеры 1ч и /3 произвольны); точка £ находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F численно F = сХ, где с—коэффициент жесткости пружины, X—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q,
а на кривошип 0\А — пара сил с моментом М; на рис. 2—9 на кривошипы 0\А и O2D действуют пары сил с моментами М| и М2. Определить, чему равна при равновесии деформация к пружины, и указать, растянута пружина или сжата. Значения всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, Mi, М2 — в ньютонометрах.
Построение чертежа начинать со стержня, направление которого определяется углом а; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10, а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,6, где одновременно иначе изображены направляющие).
Задача Д11
Механическая система состоит из тел 1, 2, ..., 5 весом соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R[ = R, г\ = 0,4/?, R2 = R, гч = 0,8/?. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R. На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами Afb М2, приложенные к блокам 1 и 2\ когда Af<0, направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформи рована. Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. «Указания»).
Прочерк в столбцах таблицы, где заданы веса , означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; для колес, обозначенных номером 4, Р\ — их общий вес (вес платформы такой тележки не учитывается).
Задача Д12
Механизм, расположенный в вертикальной плоскости (рис. Д12.0 — Д12.9), состоит из ступенчатых колес / и 2 с радиусами Ri = 0,4 м, Г| = 0,2 м, /?2 = 0,5 м, г2 = 0,3 м, имеющих неподвижные оси вращения; однородного стержня 3 длиной /=1,2 м, закрепленного шарниром на одном из концов; грузов 4 к 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние АВ = 2//3. Стержень 3 соединен с колесом 2 невесомым стержнем 6. Колеса / и 2 или находятся в зацеплении (рис. О—4), или соединены невесомым стержнем 7 (рис. 5—9). К колесам и стержню 3 прикреплены
пружины. В табл. Д12 заданы массы т, тел (кг) и коэффициенты жесткости Ci пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже
эти тела и пружины не изображать); в результате в каждом конкрет ном варианте получается довольно простой механизм, содержащий три или даже два тела. Стержень 6 или 7 входит в состав механизма, когда в него входят оба тела, соединенные этим стержнем. В положениях, изображенных на рисунках, механизм находится в равновесии. Определить частоту и период малых колебаний системы около положения равновесия. Найти также, чему равно статическое удлинение (сжатие) пружины Хст в положении равновесия. При подсчетах считать колеса 1 и 2 сплошными однородными
цилиндрами радиусов Ri и R2 соответственно. Рассмотрим два примера решения этой задачи.
- Для комментирования войдите или зарегистрируйтесь
Контакты - помощь студентам
Пн - Вскр 900-2200
39-58-68-649
bovaliservice
zakaz [at] reshuzadachi [dot] ru
+375 29 2560343
+7 965 1438010Готовые решения задач
Сотрудничество
Вниманию авторов студенческих работ! Приглашаем к долгосрочному и взаимовыгодному сотрудничеству кандидатов наук, аспирантов, инженеров и других специалистов. Горячие вакансии: геодезия, термех и сопромат строительного профиля БНТУ, спецпредметы БГИУР (проектирование РЭС, СВЧ, антенны) и другие. Ждем ваше резюме...
Помощь заочникам
Готовые решения задач, дополнительные шпаргалки, методички, находятся в свободном доступе тут
Задача ДЗ
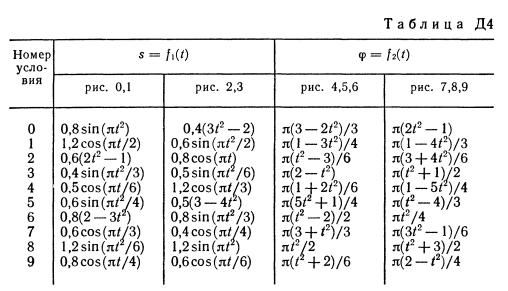
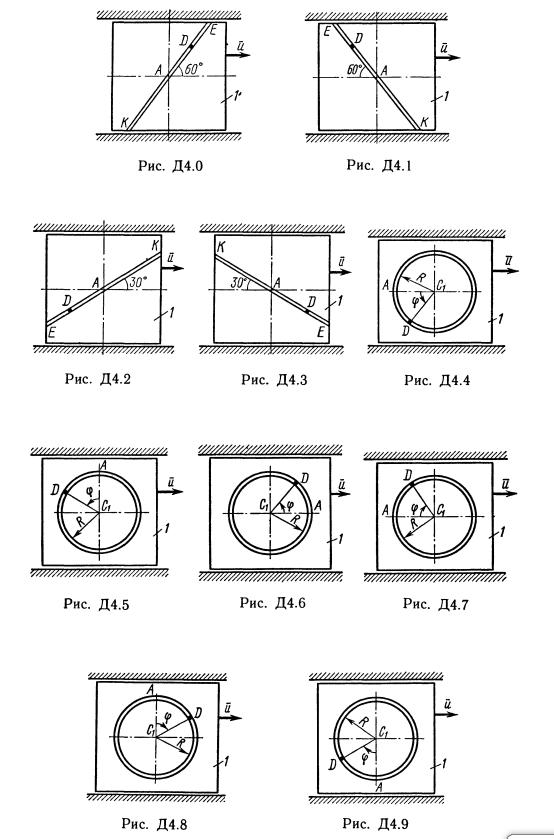
Механическая система состоит из грузов массой 2 кг и Di массой ш2 = 6 кг и из прямоугольной вертикальной плиты массой тз = 12 кг, движущейся вдоль горизонтальных направляющих (рис. ДЗ.О — Д3.9, табл. ДЗ). В момент времени, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности радиусов 0,4 м и R — 0,8 м. При движении грузов угол изменяется по закону, а угол ф2 — по закону ф2 = (0* В табл. ДЗ эти зависимости даны отдельно для рис. 0—4 и 5—9, 'где ф выражено в радианах, t — в секундах. Считая грузы материальными точками и пренебрегая всеми сопротивлениями, определить закон изменения со временем величины, указанной в таблице в столбце «Найти», т. е. хз , где хз — координата центра Сз плиты (зависимость хз = (0 определяет закон движения плиты), N — полная нормальная реакция направляющих.